教師有り学習の基本、決定木の動作を実データを使って確認してみた。
データの集合が以下の通り与えられていたとする。
(x,y)i = (x1,x2,x3,……,xk,y)i
決定木とは、従属変数x1,x2,x3.. が説明変数yにどの程度影響を与えているかを表すデータ構造を指す。説明変数yを予測するモデルであり、教師データ(x,y)iからこのモデルを生成することから「教師あり学習」に分類される。その素性がとても簡単なので教師有り学習の一番最初に出てくる。
中間ノードは根からそのノードに至るまでの質問を全て満たす説明変数xの集合に対応し、中間ノードから子ノードへの枝はその変数yiが取り得る個別の値に対応する。決定木のノードと枝はIF-THEN-ELSEに相当する。
中間ノードから子ノードへの分岐を繰り返すと、説明変数xが唯一に決まる時が来る。根から末端ノードまで辿るということは、従属変数に対応する質問を繰り返していったときの結論である。
なお、中間ノードから子ノードへ木を成長させていく際、従属変数の選び方が複数発生する。子ノードのバラつきを何らかの形で定量化し、バラつきが最も小さい従属変数を選択する。例えばバラつきの定量化手法としてエントロピーを採用する場合、親ノードの平均情報量と子ノード候補の平均情報量の差(情報利得)が最も小さい従属変数を選択する。バラつきを求める手法として”ジニ係数”を利用するものもあるらしい。
ということで、Rを使ってirisデータフレームについてSpeciesを説明変数、残りを従属変数として決定木を作成してみた。
> tree = rpart(Species~.,data=iris,method="class")
> tree
n= 150
node), split, n, loss, yval, (yprob)
* denotes terminal node
1) root 150 100 setosa (0.33333333 0.33333333 0.33333333)
2) Petal.Length< 2.45 50 0 setosa (1.00000000 0.00000000 0.00000000) *
3) Petal.Length>=2.45 100 50 versicolor (0.00000000 0.50000000 0.50000000)
6) Petal.Width< 1.75 54 5 versicolor (0.00000000 0.90740741 0.09259259) *
7) Petal.Width>=1.75 46 1 virginica (0.00000000 0.02173913 0.97826087) *
出力にインデントがかかっているので何となく木構造が見えるのだが、Rのグラフ出力機能を使ってみる。
> par(xpd=NA)
> plot(treem branch = 0.8, margin = 0.05)
> text(tree, use.n = TRUE, all=TRUE)
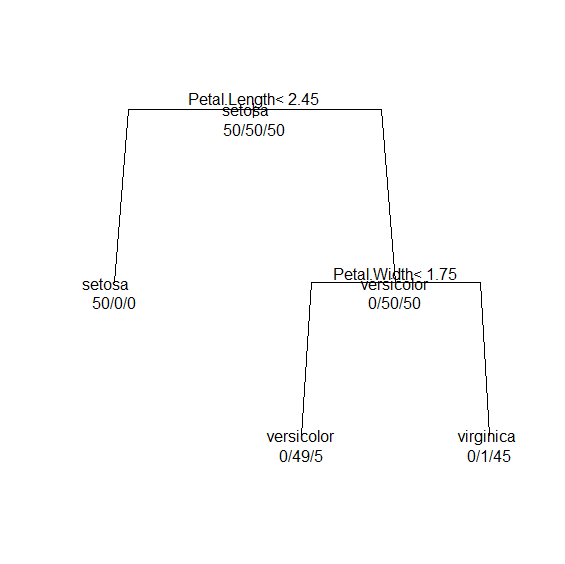
見づらい…。rpart.plotを使う。
> install.packages("rpart.plot")
> library("rpart.plot")
> rpart.plot(tree, type=1,uniform=TRUE,extra=1,under=1,faclen=0)
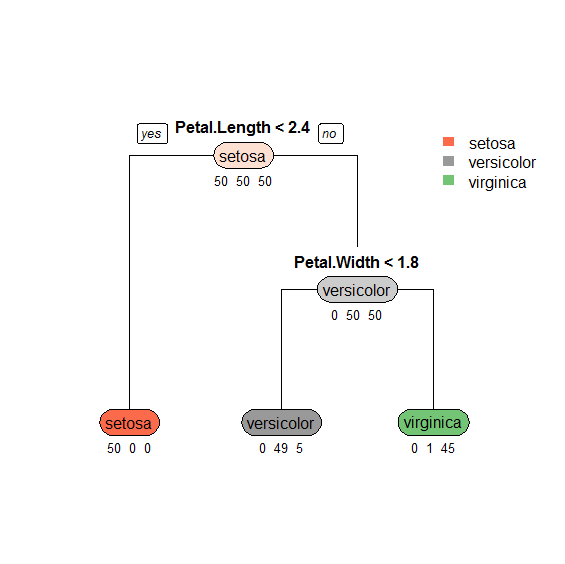
まだ見づらい…。partykitを使う。
> install.packages("partykit")
> library("partykit")
> plot(as.party(tree))
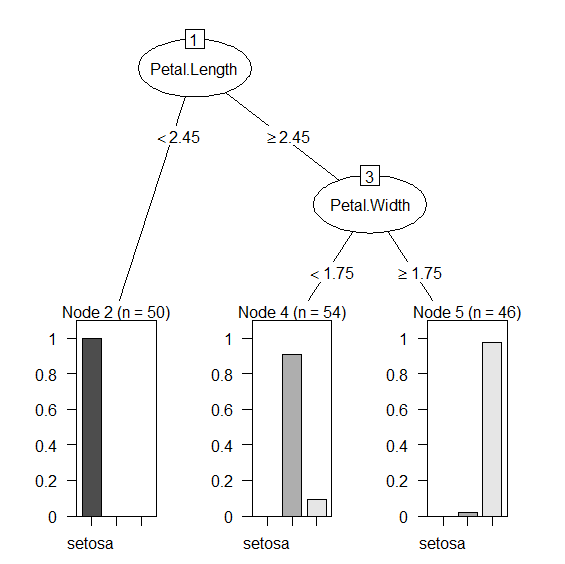
なんだか、rpart.plot だけ分岐の値が異なる気がしないでもないが…。partykitの奴は末端のラベルが全部setosaになってる気がしないでもないが…。この木の見方は以下の通り。
- 従属変数 Petal.Lengthが2.45未満のものは全て 説明変数が Speciesがsetosa
- 従属変数 Petal.Lengthが2.45以上のものは
- 従属変数 Petal.Widthが1.75未満のものは
- 説明変数 Speciesがversicolorのものが49個
- 説明変数 Speciesがvirginicaのものが5個
- 従属変数 Petal.Widthが1.75以上のものは
- 説明変数 Speciesがversicolorのものが1個
- 説明変数 Speciesがvirginicaのものが45個
- 従属変数 Petal.Widthが1.75未満のものは
従属変数 Petal.Length と Petal.Width がわかれば、この木を辿ることで 説明変数 Species が何になるか予測できる。決定木のエントリというよりRの使い方みたいなエントリになってしまったな。




