線形サポートベクトル分類器で画像認識する流れを理解したので、
定着させるために記事にしてみます。
当然、モデルの数学的な理解がないとモデルを解釈することは不可能だし、
正しいハイパーパラメータを設定することも不可能なので、数学的な理解は不可欠。
NumPy、pandas、matplotlibに慣れないと、そこまで行くのに時間がかかります。
こちらはPythonプログラミングの領域なので、数こなして慣れる他ないです。
機械学習用のサンプル画像で有名なMNISTを使ってNumPy、pandasの練習。
手書き文字認識用の画像データを読み込んでみる。サイズは28×28。各々1byte。
MNISTの手書き文字認識画像の読み込み
まず読み込んでみて、データの形を出力してみる。
X_trainは、要素が3個のTupleが返る。3次。
1番外が60000。28×28の2次のndarrayが60000個入っていると読む。
1枚目の画像データはX_train[0]によりアクセスできる。
import tensorflow as tf
minst = tf.keras.datasets.mnist
(X_train,y_train),(X_test,y_test) = mnist.load_data()
print(X_train.shape)
# (60000, 28, 28)
y_trainは要素が1個のTupleが返る。1次。
1枚目から60000枚目までの画像が0から9のいずれに分類されたかが入っている。
y_train[0]が4なら、1枚目の画像が4に分類された、という意味。
print(y_train.shape)
# (60000,)
データセットの選択
X_train,y_train、X_test,y_testから、値が5または8のものだけのViewを取得する。
そのために、まず値が5または8のものだけのインデックスを取得する。
NumPyのwhereはndarrayのうち条件を満たす要素のインデックスを返す。
X_trainに入っている60000件の2d arrayのうち、
値が5または8のインデックス(0-59999)を取得するのは以下。
index_train = np.where((X_train==5)|(X_train==8))
print(index_train)
# (array([ 0, 11, 17, ..., 59995, 59997, 59999]),)
index_test = np.where((X_test==5)|(X_test==8))
print(index_test)
# (array([ 8, 15, 23, ..., 9988, 9991, 9998]),)
インデックスを使って絞り込む。
X_train,y_train = X_train[index_train],y_train[index_train]
X_test,y_test = X_test[index_test],y_test[index_test]
print(X_train.shape)
# (11272, 28, 28)
print(X_test.shape)
# (1866, 28, 28)
前処理
0-255の間の値を0-1の間の値に変換する(正規化)。
28×28の画像(2darray)を1×784(1darray)に整形する(平坦化)。
X_train,X_test = X_train / 255.0, X_test / 255.0
X_train = X_train.reshape(X_train.shape[0], X_train.shape[1] * X_train.shape[2])
X_test = X_test.reshape(X_test.shape[0], X_test.shape[1] * X_test.shape[2])
ベストなハイパーパラメータの選択
線形サポートベクトル分類器を作成する。
from sklearn.svm import LinearSVC
linsvc = LinearSVC(loss="squared_hinge",penalty="l1",dual=False)
線形サポートベクトル分類器のハイパーパラメータCの選択
逆正則化パラメータCをGridSearchCVで探す。MBP2013Laterで学習(fit)に5分くらいかかった。
GridSearchCVからはC=0.2がbestと返ってくる。
from sklearn.model_selection import GridSearchCV
param_grid = {"C":[0.025,0.05,0.1,0.2,0.4]}
model = GridSearchCV(estimator=linsvc, param_grid=param_grid,cv=5,scoring="accuracy",return_train_score=True)
model.fit(X_train,y_train)
print(model.cv_results_["mean_train_score"])
# array([0.96291693, 0.96775192, 0.97059085, 0.97340754, 0.97626859])
print(model.cv.results_["mean_test_score"])
# array([0.95626331, 0.95990064, 0.96158623, 0.9625621 , 0.96105394])
print(model.best_params_)
# {'C': 0.2}
学習、精度評価
C=0.2を使って新しく学習させる。
linsvc = LinearSVC(loss="squared_hinge",penalty="l1",dual=False,C=0.2)
linsvc.fit(X_train,y_train)
訓練データ、テストデータに対して正答率を求める。
訓練データについて97.2%、テストデータについて96.2%。
過学習すると訓練データが高くテストデータが低くなる。
from sklearn.metrics import accuracy_score
pred_train = linsvc_best.predict(X_train)
acc = accuracy_score(y_true = y_train,y_pred = pred_train)
print(acc)
# 0.9723207948899929
pred_test = linsvc_best.predict(X_test)
acc = accuracy_score(y_true = y_test,y_pred = pred_test)
print(acc)
# 0.9619506966773848
モデルの解釈可能性
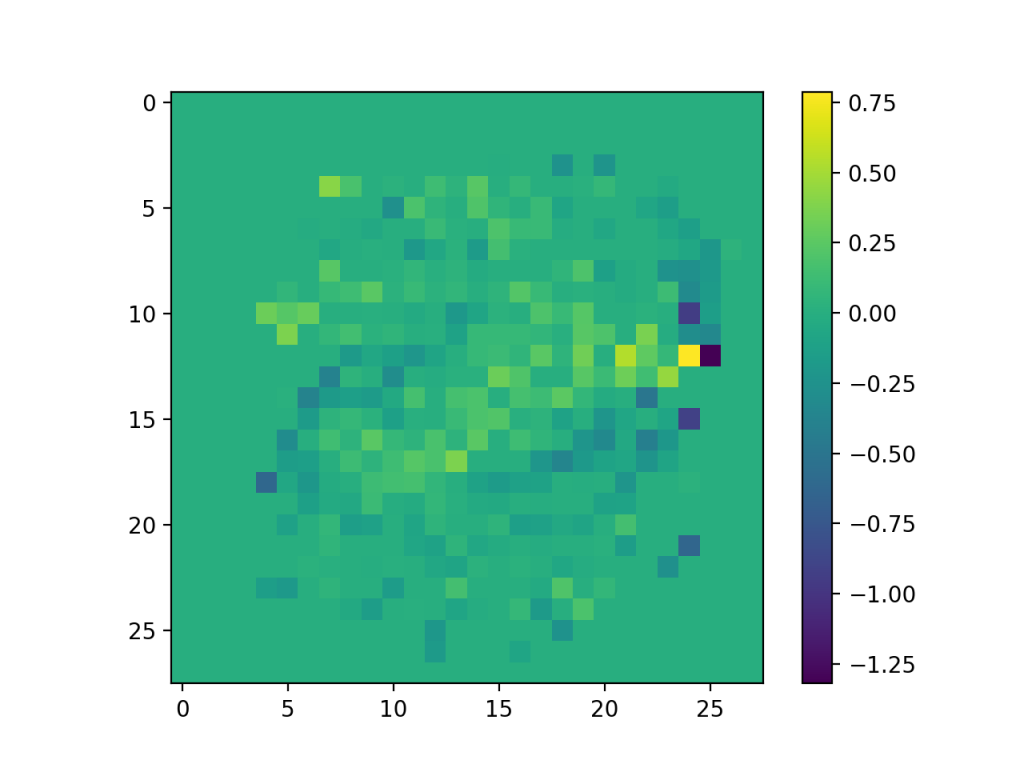
線形SVMの決定境界\(f(x)\)の係数をヒートマップっぽく表示して、どの係数を重要視しているかを確認する。
基本的に真ん中に画像が集まっているので、28×28の隅は使わないのが正しそう。
正則化パラメータによって係数の大きさを制御しているため、正則化パラメータを変えると係数が変わる。
今回のは\(L_1\)正則化なので、係数が0のものが増える..らしい(..別途調べる..)。
\(f(x) = w_0 + w_1 x_1 + w_2 x_2 + \cdots w_{784} x_{784}\)
import matplotlib.pyplot as plt
weights = linsvc_best.coef_
plt.imshow(weights.reshape(28,28))
plt.colorbar()
plt.show()