深層学習入門。Python,Numpyにも少し慣れてきたので、
Numpyだけで伝搬,逆伝搬を計算することで深層学習に慣れていく。
単に自分の理解のためだけの記事なので、誤りがあっても気にしない。
活性化関数
まず活性化関数。activation function。
3つ\(x_1,x_2,x_3\)の入力があったとする。それぞれに重み\(w_1,w_2,w_3\)がかかるとする。
ノードは入力に重みをかけた和、つまり\(w_1x_1 + w_2x_2 + w_3x_3\)を受けるものとする。
ノードは受けた値の大きさに応じて出力を返す機能を持つ。
受けた値と出力の関係（まさに関数）を活性化関数と言って、
ステップ関数,Sigmoid関数,ReLU,Softmax関数などいくつか種類がある。
Step関数,Sigmoid関数,ReLUをNumpyだけで実装してみる。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
import numpy as np import matplotlib.pyplot as plt # sigmoid function def sigmoid(x): return 1 / (1+np.exp(-x)) # step function def step(x): return np.array(x > 0, dtype=int) # ReLU def relu(x): return np.maximum(0,x) / 5 x = np.arange(-5.0,5.0,0.1) y = sigmoid(x) x = np.arange(-5.0,5.0,0.1) y1 = sigmoid(x) y2 = step(x) y3 = relu(x) plt.plot(x,y1) plt.plot(x,y2) plt.plot(x,y3) plt.ylim(-0.1,1.1) plt.show() |
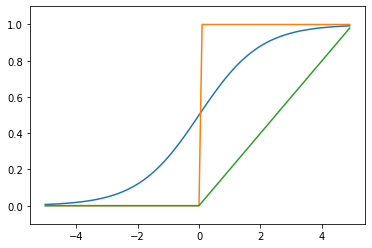
どんなに入力信号が大きくても、出力を0から1の間に押し込める。
入力が大きければ出力が大きいという意図はあるものの、
入力と出力の関係が非線形になっているものが多い。
活性化関数が線形関数だと、ネットワークを重ねていったとしても、
ネットワークの最初の入り口と最後の出口を見たとして、1つの線形関数を通しただけ…
ということになる。つまり加算と定数倍は何回実行したとしても、
一つの定数倍、加算の計算にまとめることができる。
これだと、層を重ねる意味がなくなってしまう。
活性化関数が非線形だと、重ねた活性化関数をまとめることはできず、
複雑な入出力を表現できるため、活性化関数として非線形関数を使用する。