Excelでカイ二乗分布曲線を描く

Excelは統計関数が充実している

一緒にPythonとRを習得した方が良いのだろうけど、Excelでも結構やれるらしいので、
Excelでカイ二乗分布曲線を描いてみる。

やり方

カイ二乗分布の確率密度関数は以下の通り。
\begin{eqnarray}
f_n(x) = \frac{1}{2^{\frac{n}{2}}\Gamma({\frac{n}{2}})}x^{\frac{n}{2}-1}e^{-\frac{x}{2}}
\end{eqnarray}
Excelには確率密度関数と累積分布関数を取得する関数が標準で備わっている。

\(x\)と\(n\)の2変数関数なので、行,列をそれぞれに割り当ててクロスするところが値。
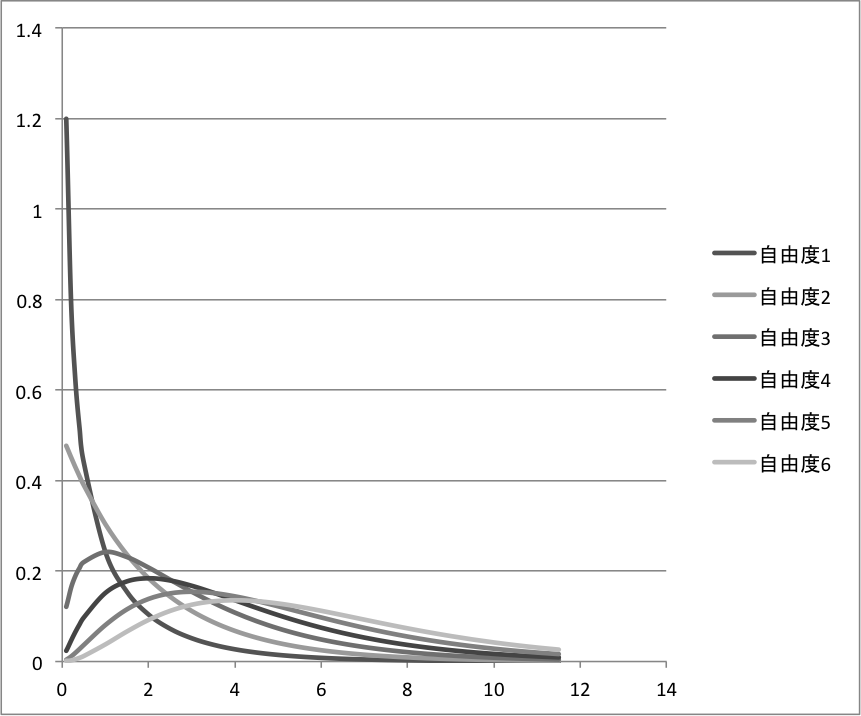
自由度=1のとき\(x=0\)で無限大に発散するのに注意が必要。
\(0 \lt x \lt 1\)の区間で形が変わるのでそれも注意が必要。

確率密度関数のグラフをプロットすると以下のようになる。

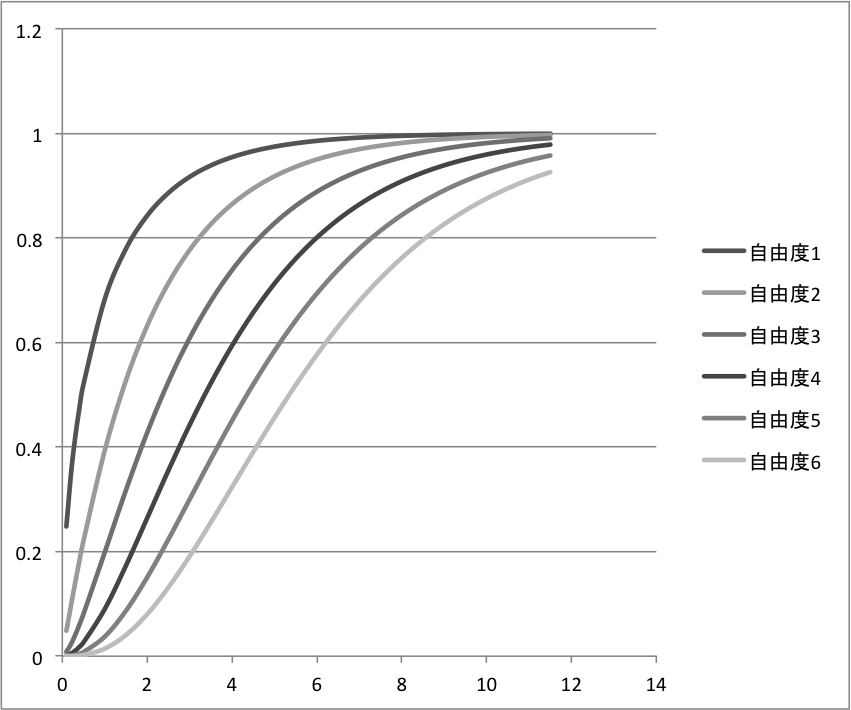
累積分布関数のグラフは以下。
確率密度関数の積分グラフですかね。

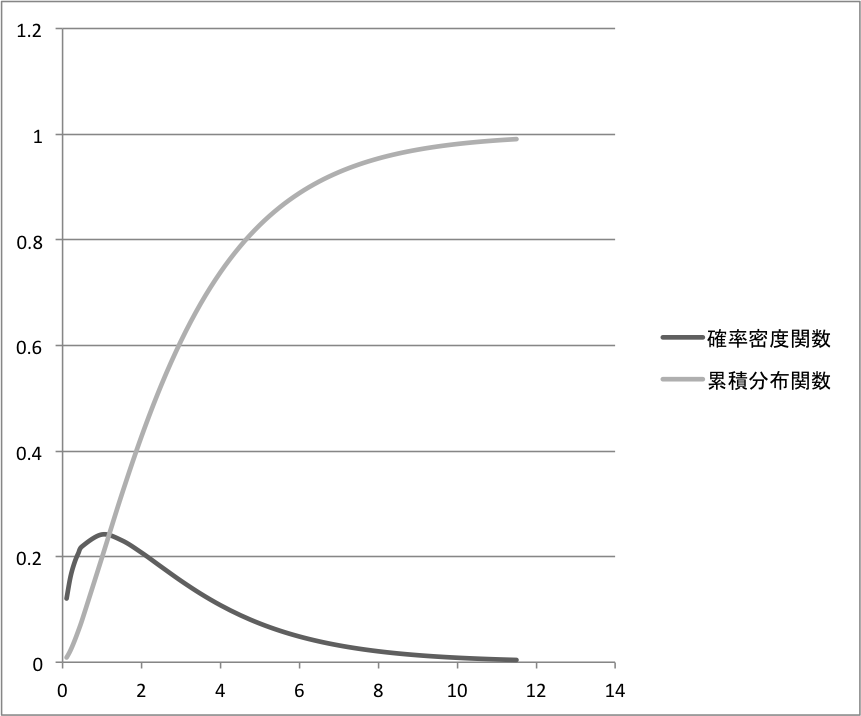
自由度=3のときの確率密度関数のグラフと累積分布関数のグラフを並べてみる。
\(x=7.5\)くらいに確率密度関数の値が\(0.025\)くらいになる。
\(x \lt 7.5\)の面積が\(0.975\)くらい、または\(x \gt 7.5\)の面積が\(0.025\)くらい。
つまり、\(\int_{0}^{7.5}f_3(x) = 0.975\)くらいで、\(\int_{7.5}^{\infty}f_3(x) = 0.025\)という意味。

\(x=7.5\)くらいのとき累積分布関数の値が\(0.975\)くらいになる。
標準正規分布に従う3個の変数の二乗和の97.5%は7.5より小さい。