そろそろ適当なデータを見つけてきて手法を試すのとは別に、
自力でデータを作って試してみたいと思い、NumPyを使った生成法を調べてみた。
一口に乱数といっても、正規分布に従う標本の生成のこと。
多次元正規分布に従う標本をmultivariate_normalで生成して表示してみる。
1次元正規分布に従う標本
その前に普通の乱数。
平均\(\mu\)、標準偏差\(\sigma\)の正規分布\(N(\mu,\sigma)\)に従う標本の生成。
numpy.random.normal(\(\mu,\sigma,n\))。
以下、\(\mu=50,\sigma=10\)として1000個の標本を作って、
階級数100のヒストグラムとして表示する。
import numpy as np
import matplotlib.pyplot as plt
values = np.random.normal(50, 10,1000)
plt .hist(values,bins=100)

多次元正規分布に従う標本
多次元の乱数を作るのに必要なのは、
各次元における平均\(\mu=\begin{pmatrix}\mu_1 \\ \mu_2 \end{pmatrix}\)と、分散共分散行列\(\sum=\begin{pmatrix}\sigma_{11} & \sigma_{21} \\ \sigma_{12} & \sigma_{22}\end{pmatrix}\)。
ちなみに、\(\sum=\begin{pmatrix}\sigma_{11} & \sigma_{21} \\ \sigma_{12} & \sigma_{22}\end{pmatrix} = \begin{pmatrix} \sigma_1^2 & \sigma_{21} \\ \sigma_{12} & \sigma_2^2 \end{pmatrix} =
\begin{pmatrix} \sigma_1^2 & Cov(X_1,X_2) \\ Cov(X_2,X_1) & \sigma_2^2 \end{pmatrix} \)。
対角に分散、それ以外にクロスする共分散が入る。
共分散は昔書いてた。
\begin{eqnarray}
r_{xy} &=& \frac{C_{xy}}{S_x S_y} \\
&=& \frac{\sum_{i=1}^n(x_i-\bar{x})(y_i-\bar{y})/n}{\sqrt{\sum_{i=1}^n{(x_i-\bar{x})^2}/n} \sqrt{\sum_{i=1}^n{(y_i-\bar{y})^2}/n}} \\
&=& \frac{\sum_{i=1}^n(x_i-\bar{x})(y_i-\bar{y})}{\sqrt{\sum_{i=1}^n{(x_i-\bar{x})^2}} \sqrt{\sum_{i=1}^n{(y_i-\bar{y})^2}}} \\
\end{eqnarray}
共分散と相関係数の定義について過去に書いていた。 そもそも共分散が発生するのは、2つの確率変数が連動して動くから。 2つの確率変数が独立している場合は、共分散、相関係数共にゼロ。 共分散の定義 まず、共分散、相関係数の定義はこの通り。 2次元のデータ\((x_1,y_1),(x_2,y_2),\cdots,(x_n,y_n)\)が与えられた場合、 変数\(x\)と\(y\)の相関係数\(r_{xy}\)は、それぞれの標準偏差\(S_x,S_y\)と、共分散\(C_{xy}\)を使って以下となる。 \begin{eqnarray} r_{xy} &=& \
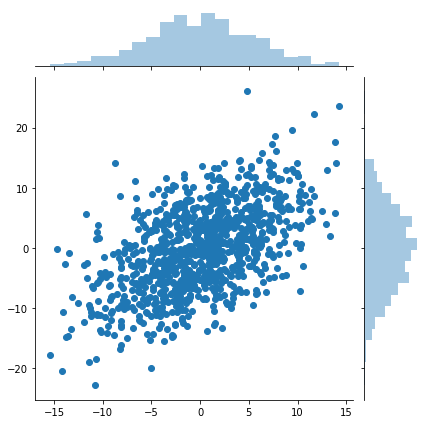
平均\(\mu=\begin{pmatrix} 0 \\ 0\end{pmatrix}\)、分散共分散行列\(\sum=\begin{pmatrix}30 & 20 \\ 20 & 50\end{pmatrix}\)の2次元正規分布に従う標本を1000個作る。
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
mu = [0,0]
sigma = [[30,20],[20,50]]
values = np.random.multivariate_normal(mu, sigma, 1000)
sns.jointplot(x=values[:,0],y=values[:,1])
散布図とヒストグラムを良い感じに表示してくれるseaborn.jointplotを使って表示してみる。
第1軸、第2軸とも平均は0っぽい。
第1軸は-15から15、第2軸は-25から25くらいが入っていて、対角とあってそう。