2変数関数\(f(x_0,x_1)\)を各変数で偏微分する。
地点\((i,j)\)におけるベクトル\((\frac{\partial f(x_0,j)}{\partial x_0},\frac{\partial f(i,x_1)}{\partial x_1})\)を全地点で記録していき、ベクトル場を得る。
このベクトル場が勾配(gradient)。
\(f(x_0,x_1)=x_0^2+x_1^2\)について、\(-4.0 \le x_0 \le 4.0\)、\(-4.0 \le x_1 \le 4.0\)の範囲で、
勾配を求めてみる。また、勾配を可視化してみる。
まず、2変数関数\(f(x_0,x_1)\)の偏微分係数を求める関数の定義。
\((3.0,3.0)\)の偏微分係数は\((6.00..,6.00..)\)。
def numerical_gradient(f, x):
h = 10e-4
grad = np.zeros_like(x)
for idx in range(x.size):
tmp_val = x[idx]
x[idx] = tmp_val + h
fxh1 = f(x)
x[idx] = tmp_val - h
fxh2 = f(x)
grad[idx] = (fxh1 - fxh2) / 2*h
x[idx] = tmp_val
return grad
def function2(x):
return x[0]**2 + x[1]**2
p = np.array([3.0,3.0])
v = numerical_gradient(function2, p)
v # array([6.e-06, 6.e-06])
\(-4.0 \le x_0 \le 4.0\)、\(-4.0 \le x_1 \le 4.0\)の範囲(\(0.5\)刻み)で偏微分係数を求めて、
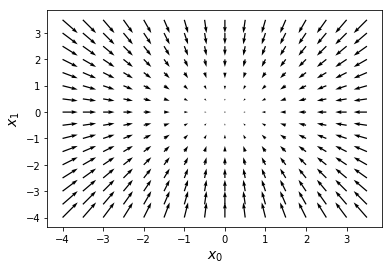
ベクトル場っぽく表示してみる。matplotlibのquiver()は便利。
各地点において関数の値を最も増やす方向が表示されている。
w_range = 4
dw = 0.5
w0 = np.arange(-w_range, w_range, dw)
w1 = np.arange(-w_range, w_range, dw)
wn = w0.shape[0]
diff_w0 = np.zeros((len(w0), len(w1)))
diff_w1 = np.zeros((len(w0), len(w1)))
for i0 in range(wn):
for i1 in range(wn):
d = numerical_gradient(function2, np.array([ w0[i0], w1[i1] ]))
diff_w0[i1, i0], diff_w1[i1, i0] = (d[0], d[1])
plt.xlabel('$x_0$',fontsize=14) #x軸のラベル
plt.ylabel('$x_1$',fontsize=14) #y軸のラベル
plt.xticks(range(-w_range,w_range+1,1)) #x軸に表示する値
plt.yticks(range(-w_range,w_range+1,1)) #y軸に表示する値
plt.quiver(w0, w1, diff_w0, diff_w1)
plt.show()
値が大きい方向に矢印が向いている。例えば\((-3.0,3.0)\)における偏微分係数は\((-6.0,6.0)\)。
左上方向へのベクトル。

参考にしている本にはことわりが書いてあり、勾配にマイナスをつけたものを図にしている。
その場合、関数の値を最も減らす方向が表示されることになる。
各地点において、この勾配を参照することで、どちらに移動すれば関数の値を最も小さくできるかがわかる。