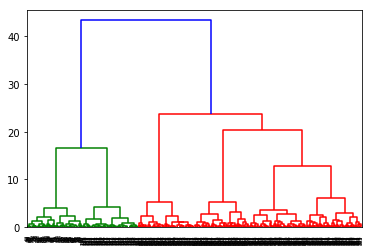
前回適当に作ったデータを使って階層型クラスタリングを試してみる。
階層型クラスタリングの様子をdendrogramというツールを使って可視化できるのと、
クラスタ間距離の違いによってクラスタの作られ方が大きく変化することを
dendrogramの違いを見ながら確認してみる。
テストデータを作る
データは前回と同様に以下のように作る。
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
mu = [[0,0], [20,20], [50,50], [40,30], [40,10], [20,40]]
sigma = [ [[30,20],[20,50]], [[20,30],[10,20]], [[60,40],[20,20]], [[60,20],[20,60]] ,[[30,10],[10,30]],[[50,20],[20,50]] ]
points = 100
clusteres = []
for index in range(len(mu)):
cluster = np.random.multivariate_normal(mu[index], sigma[index], points)
dig = np.full((points,1),index+1, dtype=int)
cluster = np.hstack((cluster,dig))
clusteres = np.r_[clusteres,cluster] if len(clusteres) > 0 else cluster
plt.scatter(x=clusteres[:,0], y=clusteres[:,1],c=clusteres[:,2])
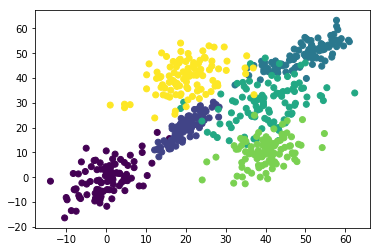
dendrogram
階層型クラスタリングの可視化を行う方法の1つとしてdendrogramがある。
葉(=各データポイント)から始まり、クラスタがまとまっていく様を木構造で表した図。
根は全てのデータポイントを1つのクラスタで表した状態。
左部分木と右部分木に1度別れるところが2つのクラスタに別れた状態。
グラフの縦軸はクラスタ間距離を表していて、dendrogramによって各クラスタの離れ度合いがわかる。
from sklearn.preprocessing import StandardScaler
from scipy.cluster.hierarchy import linkage, dendrogram, fcluster
SS = StandardScaler()
scaled_clusters = SS.fit_transform(clusteres)
result = linkage(scaled_clusters, method = "ward")
dendrogram(result)
plt.show()
クラスタを作っていく際にどうクラスタ間距離を設定するかで木の構造がだいぶ変わってくる。
空間拡散性
以下はクラスタ間距離として最短距離法を使った場合。
(クラスタ間距離としてそれぞれに含まれるデータポイント間の距離の最小値)
1度併合してクラスタが大きくなると、次に、そのクラスタと隣のクラスタがくっつきやすい。
(データ数が多すぎてよくわからないけれど)下のdendrogramは
右、その1つ左、その1つ左…というように、右から順番に併合する傾向が強いのがわかる。
つまり1度クラスタが作られると、そのクラスタは次のクラスタになりやすい。
1度作られたクラスタは次にクラスタになりにくい性質、
(=あちこちでバランスよくクラスタが作られていって最後にそれぞれがまとまる性質)
を空間拡散性というらしい。ほぅ。下の図は空間拡張性が無いことを表す。
クラスタ数を多くしていったとき、空間拡張性がないと”でかいクラスタ”と”小さいクラスタ”が共存する
アンバランスな構造になりそう。
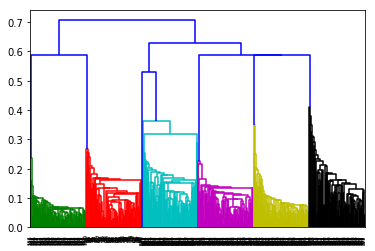
距離の単調性
以下は重心法を使った場合。
重心法というのは、クラスタとクラスタの距離として各クラスタの重心間の距離を使う方法。
まぁ妥当な距離な感じがするが..。
本来は、同時多発的にクラスタが出来上がり、より大きくなるにつれて、
より遠いクラスタと併合するのが”あるべき姿”なのだけれども、
1度クラスタがくっつくと、他のクラスタとの距離が以前よりも小さくなってしまう状態が発生する。
距離の単調性がない、というらしい..。むむ.
dendrogramの縦方向はクラスタ間距離なので、
距離の単調性があるのであれば、左右の部分木は両方とも下方向に伸びるはず。
無いのであれば、左右のいずれかが上方向に伸びる。
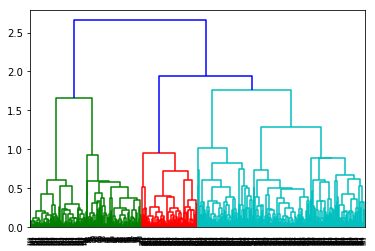
ward法を使った場合
以下はWard法を使った場合。詳細は以下。無茶苦茶面倒臭い。
階層型クラスタリングについてわかりやすい解説を聞いたので頭の中にあるものを書き出してみます。 (せっかく聞いたシャープな解説が台無しになってしまっているかと思いますが...) 本当はもっとアクティブなアウトプット方法があれば良いのですが、今のところはブログしかないのと、 WordPressのエントリという単位が、アウトプットの量として個人的に丁度良いなと思いますので。 初学なので解釈の誤りとか検討不足があるかと思いますが、本日も書いていきます! 試しに実行してみるためのデータを作る面倒さの洗礼を受けまして、 実際に試すのは別記事になります。 [clink url="htt
空間拡散性、距離の単調性があって(バランス木という言葉は全然違うが..)
バランス良く木ができている。
データ数が多すぎて全然見えないけど…