参考書籍を読んでいく. 今回はロジスティック回帰.
未知のサンプルのクラスの所属確率を見積もることができる, という重要なことが書かれている.
また重みの学習は勾配降下法のフレームワークの中で統一されていて一連の理解が進む.
一度は理解しておいた方が良い内容だと思った.
パーセプトロンとADALINE
線形和\(z=w^T\)を考えたとき 「サンプル\(x\)が決定境界の上にある」 というのは\(w^Tx=0\).
\(w^T x > 0\), \(w^T x < 0\) を決定境界の 「こちら側」 か 「向こう側」 か対応させる.
パーセプトロンのアイデアは以下の通り.
- 線形和 \(z=w^T x\)を決定境界とし, \(\phi(z)\in (-1,+1)\)を予測ラベルとする
- 予測が誤った回数, つまり真のラベルと予測ラベルの差の合計がゼロになるように\(w\)を学習する
- \(\phi(z)\)はステップ関数で連続ではないので解析的な式の変形ができない
- 決定境界により完全に分離できなければ学習が収束することはない
決定境界から離れている度合いを連続で凸な関数として定義し,
その関数が極小となる\(w\)を求めていこう, というアイデアに拡張したのがADALINE.
- \(\phi(z) = z\).
- コスト関数\(J(w) = \frac{1}{2} \sum_i \left( \hat{y^{(i)} – \phi ( z^{(i)})} \right)^2 \)
- トレーニングセット全体から\(J(w)\)の極小化を考えることが可能. (勾配降下法)
- トレーニングセットの一部を使って\(J(w)\)の極小化を考え, 他のトレーニングセットで反復することも可能. (確率的勾配降下法)
ロジスティック回帰
決定境界を表す線形和\(z=w^T x\)について\(\phi(z) \in (\mathbb{R}| 0 \leq z \leq +1)\)を考える.
線形和\(z\)がクラス1に分類される確率を表す\(\phi(z)\)を考える.
\(\phi(z)\)をどう作るのか
線形和を\(0\)から\(1\)の実数全体に変換する関数を考える.
オッズ比の対数をとったロジット関数\(logit(p)\)を使う.
ここで \(p\)は\(x\)が与えられたときにサンプルデータがクラス1に属する確率.
\begin{eqnarray}
logit(p(y=1 | x)) &=& \log \frac{p}{1-p} \\
&=& w_0 x_0 + w_w x_w + \cdots + w_m x_m \\
&=& \sum_{i=0}^m w_i x_i \\
&=& w^T x
\end{eqnarray}
つまり, 線形和\(z = w^T x \in (\mathbb{R} | 0 \leq z \leq 1) \)
\(p\)は未知であるということが重要. この式から\(p\)を予測していく.
\(f(p) = \log \frac{p}{1-p}\) の逆関数が分かれば良い.
\begin{eqnarray}
f(p) &=& \log \frac{p}{1-p} \\
e^{f(p)} &=& \frac{p}{1-p} \\
(1-p)e^{f(p)} &=& p \\
e^{f(p)} &=& p(1+e^{f(p)}) \\
p &=& \frac{e^{f(p)}}{1+e^{f(p)}} \\
p &=& \frac{1}{1+e^{-f(p)}}
\end{eqnarray}
\(f(p)=z\)としていたので以下のようになる.
(zとpが混在していてたぶん数式としての表現は間違ってる.. )
\begin{eqnarray}
p &=& \frac{1}{1+e^{-z}}
\end{eqnarray}
\(p\)は確率なので\(p \in (\mathbb{R}|0 \leq p \leq 1)\).
\(\phi(z) \in (\mathbb{R}|0 \leq p \leq 1) \)とすると,
\begin{eqnarray}
\phi(z) = \frac{1}{1+e^{-z}}
\end{eqnarray}
\(z-\phi(z)\)をGeoGebraでプロットすると以下のような感じ.
\(z\)を大きくしていくと\(\phi(z)\)は限りなく\(1\)に近づく.
\(z\)を小さくしていくと\(\phi(z)\)は限りなく\(0\)に近づく.
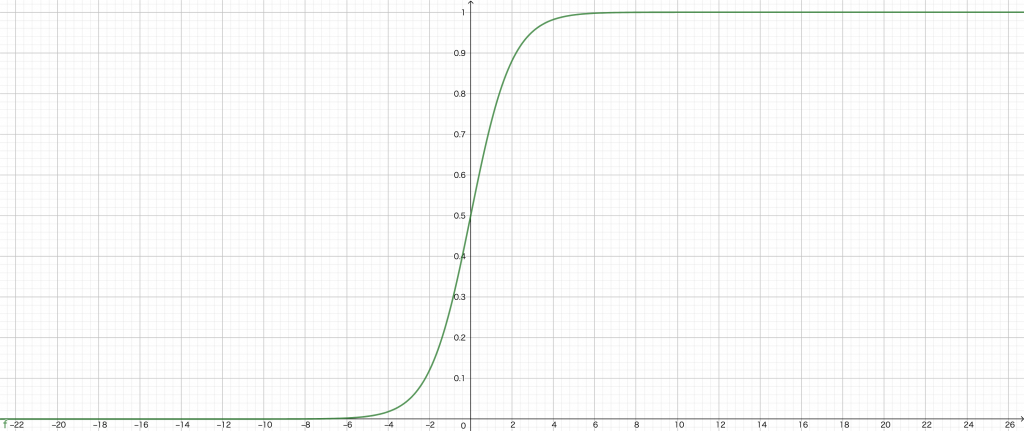
\(\phi(z)=\)の出力は正事象が起こる確率であると解釈される.
\(\phi(z)=0.8\)である場合, 80%の確率で正事象が起こり,20%の確率で正事象が起こらないことを表す.
トレーニングデータからパラメタを学習し, ある\(\phi(z)\)が得られたとして,
未知のサンプルのクラスの所属関係を確率で見積もることができる.
天気予報で晴れの確率70%、晴れでない確率30%のように.
予測の際に,クラスの所属関係の確率を見積もることができるのが神がかるレベルで重要!!
もし\(\phi(z)\)を2値分類に当てはめるのであれば,
\(\phi(z)=0.5\)を境に上半分を\(1\)、下半分を\(0\)と予測するものとする.
\begin{eqnarray}
\hat{y} = \begin{cases}
1 & \phi(z) \ge 0.5 \\
0 & \phi(z) \lt 0.5
\end{cases}
\end{eqnarray}
それって, \(z=0\)を境に左半分, 右半分に割り付けるのと同じなので,
\begin{eqnarray}
\hat{y} = \begin{cases}
1 & z \ge 0 \\
0 & z \lt 0
\end{cases}
\end{eqnarray}
ロジスティック回帰の重みの学習
では\(w\)をどうやって学習するか.
式をイジるだけで面倒なだけで,これ以上は洞察得られないなと思うので,
流れだけ書いてみる.
学生時代に形態素解析っぽい何かのアルゴリズムを考えたことがあって,
形態素どうしのベターな接続を求め際に, 接続コストをコーパスから作った確率で表して,
尤度を最大化する問題として解いた記憶があって, 今更合点が行くという謎.
勉強不足で尤度最大化のアイデアがあってそうした訳ではないので, もっと勉強していたらよかったな..と.
ADALINEの説明の中で, 真の値と予測値の差の2乗誤差をコスト関数として,
連続で凸な関数の極小化の問題として\(w\)を求めていった.
ロジスティック回帰の場合, 予測は\(\phi(z)\)も連続で凸な関数なので,
同じロジックで\(w\)を求めることもできる.
コスト関数\(J(w)\)は同様に以下.
\begin{eqnarray}
J(w) &=& \sum_i \frac{1}{2} \left( \phi(z^{(i)}) – y^{(i)} \right)^2
\end{eqnarray}
\(\phi(z)=\frac{1}{1+e^{-z}}\)だと, これを解析的に微分するのは不可能.
トレーニングデータが\(m\)個あった場合に\(i\)番目のトレーニングデータにおける確率は以下.
\(x\)も\(w\)もパラメタですよ,って書き方.
\begin{eqnarray}
P(y|x;w)=P(y^{(i)}|x^{(i)};w)
\end{eqnarray}
求めたいのは, 全てのトレーニングデータについて\(P(y)\)の積が最大になる\(w\).
積,つまり尤度を書き下すと以下のようになる.
\begin{eqnarray}
L(w) &=& \prod_{i=1}^m \left( P(y^{(i)}) | x^{(i)};w \right) \\
&=& \prod_{i=1}^m \left( \phi(z^{(i)}) \right)^{y^{(i)}} + \left( 1-y^{(i)}\right) \log \left( 1-\phi(z^{(i)}) \right)
\end{eqnarray}
尤度そのものの最大化するよりも対数をとったものを最大化する方が楽になる.
(対数をとると指数の肩が定数倍になり積が和になる. 相当簡単になる. )
\begin{eqnarray}
l(w) &=& \log L(w) \\
&=& \sum_{i=1}^{n} \left( y^{(i)} \log( \phi(z^{(i)}) ) + (1-y^{(i)}) \log (1-\phi(z^{(i)})) \right)
\end{eqnarray}
これを最大化するということは, これに\(-1\)を掛けたものを最小化するということ.
そもそもコスト関数\(J(w)\)を立てて最小化しようとしていたので, これを\(J(w)\)と置いてしまう.
\begin{eqnarray}
J(w) = \sum_{i=1}^{n} \left( -y^{(i)} \log( \phi(z^{(i)}) ) – (1-y^{(i)}) \log (1-\phi(z^{(i)})) \right)
\end{eqnarray}
ADALINEの勾配降下法で, コスト関数を最小にするように\(w\)を更新していった.
つまり, \(w := w – \Delta w\)という更新をしていった.
ロジスティック回帰において, コスト関数を対数尤度で書き直していて,
対数尤度を最大化するように\(w\)を更新する.
つまり, \(w := w + \Delta w\)という更新をおこなう.
対数尤度を最大化する\(w\)を更新する話は, コスト関数を最小化する\(w\)を更新する話と同じ,
なので, 結局のところ勾配降下法と同じ式となる.
\begin{eqnarray}
\Delta w_j &:=& – \eta \frac{\partial J}{\partial w_j}
\end{eqnarray}
尤度関数の偏導関数はシグモイド関数の偏導関数を使って以下のようになるらしい. (省略)
シグモイド関数の偏導関数は以下
\begin{eqnarray}
\frac{\partial \phi(z)}{\partial z} &=& \frac{1}{\partial z} \frac{1}{1-e^{-z}} \\
&=& \frac{1}{1+e^{-1}} \left( 1- \frac{1}{1+e^{-z}} \right) \\
&=& \phi(z) (1-\phi(z))
\end{eqnarray}
対数尤度の偏導関数はシグモイド関数の偏導関数を使って以下.
\begin{eqnarray}
\frac{\partial l(w)}{\partial w_j} &=& \left( y \frac{1}{\phi(z)} – (1-y) \frac{1}{1-\phi(z)} \right) \frac{\partial}{\partial w_j} \phi(z) \\
&=& \left( y\frac{1}{\phi(z)} – (1-y) \frac{1}{1-\phi(z)} \right) \phi(z)(1-\phi(z)) \frac{\partial}{\partial w_j} z \\
&=& \left( y(1-\phi(z))-(1-y)\phi(z) \right) x_j \\
&=& \left( y-\phi(z) \right) x_i
\end{eqnarray}
コスト関数の最小化と対数尤度関数の最大化が同じ,というロジックが効いて,
ADALINEの更新と全く同じになる.
\begin{eqnarray}
w_j &:=& – \eta \frac{\partial J}{\partial w_j} \\
&=& \eta \sum_{i=1}^n \left( y^{(i)} -\phi(z^{(i)}) \right) x_j^{(i)}
\end{eqnarray}
奇跡的..





