二項分布において、\(n\)が極めて大きく、\(p\)が極めて小さくなる現実的な事象はとても多いとされる。
例えば、交通事故件数、破産件数、火災件数、砲弾命中数、遺伝子の突然変異数など。
あるECサイトにおけるLPへの到達を\(n\)、そのうちコンバージョンする確率を\(p\)などとしたとき。
(実際には、アクセス頻度が一定でないので、単純なポアソン分布でモデル化する訳ではないらしい。
ここでは単純化してアクセス頻度が一定であるという仮定をする)
超幾何分布から二項分布、そしてポアソン分布まで地続きで理解するとわかりやすい。
このケースで二項分布の式を計算しようとすると、
例えば\(N=1000\)、\(p=0.003\)、\(x=3\)であるとしたとき、
(例えば、1000回のPVがあり、3回コンバージョンした、コンバージョン確率は0.3%である、という条件)
数値計算上の誤差により演算が繊細で現実的でない。
\begin{eqnarray}
f(x) &=& {}_n C_x p^x (1-p)^{n-x} \\
&=& {}_{1000} C_3 0.003^3 (0.997)^{997}
\end{eqnarray}
ここで、\(n \rightarrow \infty, p \rightarrow 0 \)という極限を考えたとき、\(np \rightarrow \lambda\)となることを考える。
つまり、二項分布の式において以下が成り立つ。
\begin{eqnarray}
{}_n C_x p^x (1-p)^{n-x} \rightarrow e^{-\lambda} \lambda^x /x!
\end{eqnarray}
右式が確率分布であることは指数関数のマクローリン展開を使って証明できる。
(これも無茶苦茶に鮮やかで気持ちがよい..)
\begin{eqnarray}
\sum_{x} f(x ) &=& \sum_{x} e^{-\lambda} \lambda^x /x! \\
&=& e^{-\lambda} \sum_{x} \lambda^x /x! \\
&=& e^{-\lambda} \cdot e^{\lambda} \\
&=& 1
\end{eqnarray}
ポアソン分布において、期待値、分散は以下の通り。
奇跡的に、期待値も分散も同じ\(\lambda\)となる。
\begin{eqnarray}
E(X) &=& \lambda \\
V(X) &=& \lambda
\end{eqnarray}
ポアソン分布の分布図
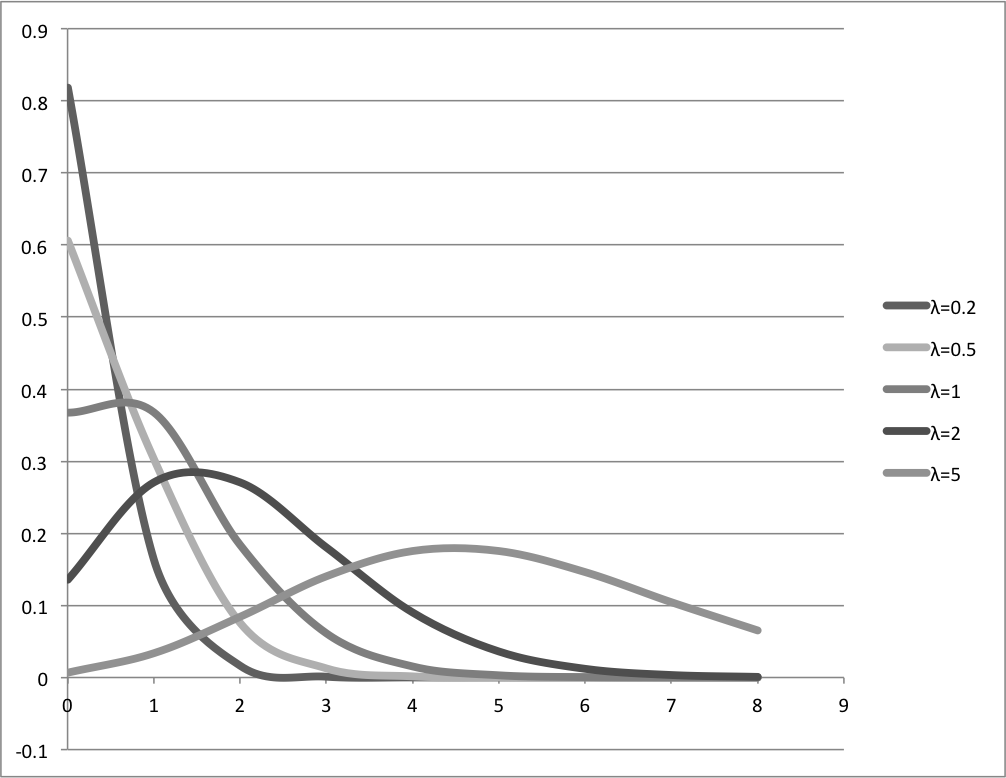
平均、分散共に\(\lambda\)ということで、分布は定数\(\lambda\)だけによって決まる。
以下、\(\lambda\)をばらけさせてExcelでプロットしてみた。
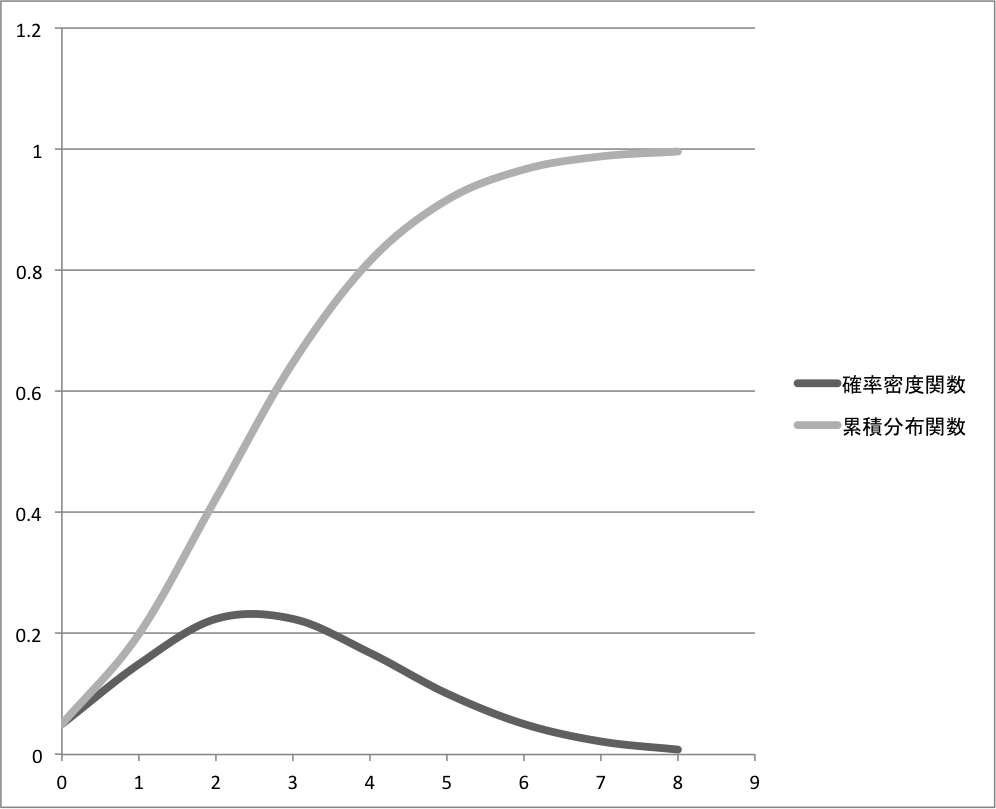
また、\(\lambda=3\)における、確率密度関数と累積分布関数を同一軸でプロットしてみる。
\(\lambda=3\)というのは、最初の\(N=1000\)、\(p=0.003\)という条件下である。
平均は\(\lambda=3\)であるから、3回コンバージョンする確率が最も大きく、
確率密度関数は右に歪んでいて、以外と3回以上コンバージョンする確率の減少は緩やか。