アンサンブル学習とかランダムフォレストに入門する前に決定木に入門する。
決定木はやっていることが直感的でわかりやすい。
決定木回帰と決定木分類。
ここよりはドメインとの連結部分が大変なんだろうと思った。
あと、Pythonは練習しないとな。
CART(Classification and Regression Tree)法(単に分類と回帰を英語にしただけだ！)
木を作るのだけれども、それが面白かったので今回と次回で書いてみる。
決定木回帰
\(y=(x-0.5)^2\)という2次曲線に従う事象があるとして、\(y\)を観測するとする。
観測による誤差が平均\(\mu=0\)、分散\(\sigma^2=0.1\)の正規分布に従うとして\(y=(x-0.5)^2+\epsilon\)。
区間\([0.0,1.0]\)の間に等間隔に存在する観測値\(x,y\)。
試行毎に\(\epsilon\)が変わってくるので、毎回異なる。
この区間に\(16\)個のデータがあるとして、それを訓練データとして使ってモデルを作る。
\(x_{train},y_{train}\)とする。
モデルの作成（学習）はfit()。
Scikit-learnに全て用意されていてデータを放り込むだけでモデルが出来る。
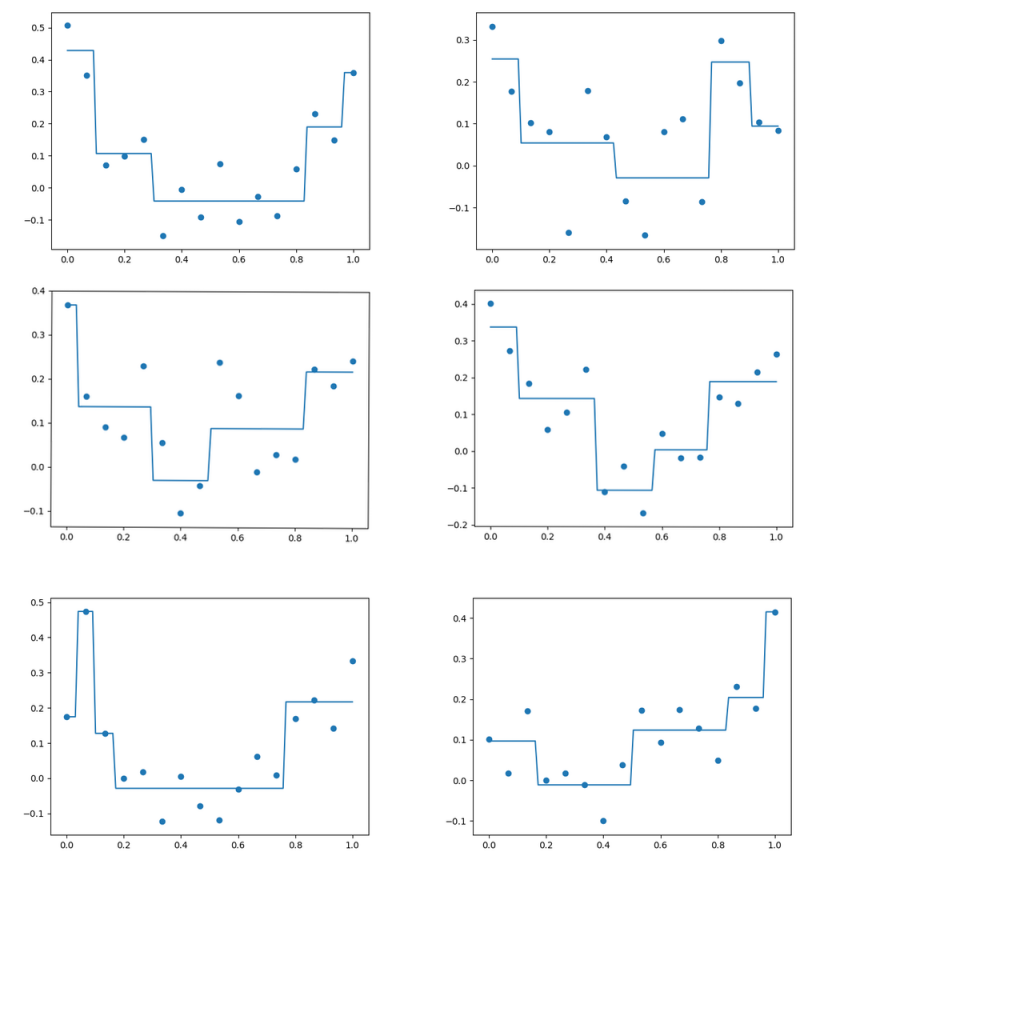
決定木の葉の最大値を\(5\)としている。他のパラメタは全部デフォルト値。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
import numpy as np # 区間[0,1]上に16個の点を等間隔に生成する X_train = np.linspace(start=0,stop=1,num=16) y_train = (X_train - 0.5) ** 2 + np.random.normal(loc=0.0,scale=0.1,size=16) # 16x1配列を1x16に整形 X_train = X_train.reshape(16,1) print(X_train) # 決定木回帰 from sklearn.tree import DecisionTreeRegressor DTR = DecisionTreeRegressor(max_leaf_nodes=5) DTR.fit(X_train,y_train) |
出来上がったモデルにテスト用データを流し込んでみる。
区間\([0.0,1.0]\)に100個のデータを発生させてpredict()を呼ぶ。
最後、訓練データと回帰結果を同じグラフを書いてみて終了。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
# 区間[0,1]上に100個の点を等間隔に生成する X_test = np.linspace(0,1,100) X_test = X_test.reshape(100,1) # 回帰! y_predict = DTR.predict(X_test) X_train = X_train.reshape(16) X_test = X_test.reshape(100) # 描画 import matplotlib.pyplot as plt plt.scatter(X_train,y_train) plt.plot(X_test,y_predict) plt.savefig('img.png') plt.show() |
葉の最大値を\(5\)としたので、木の深さが規定されて、
階段の個数が決まっている。
以下、6回分のモデルと予測の同時プロット。
\(\epsilon\)の変化により訓練データが微妙に変わるだけで、
決定木の構造がむちゃくちゃ変化するのが特徴。
それっぽく言うとロバスト性が無いとか。
訓練データによって決定木がかなり違うことを利用して、
複数の決定木から多数決で結果を得ようというのがアンサンブル学習の試み。
むー。順々に詰めていこう。
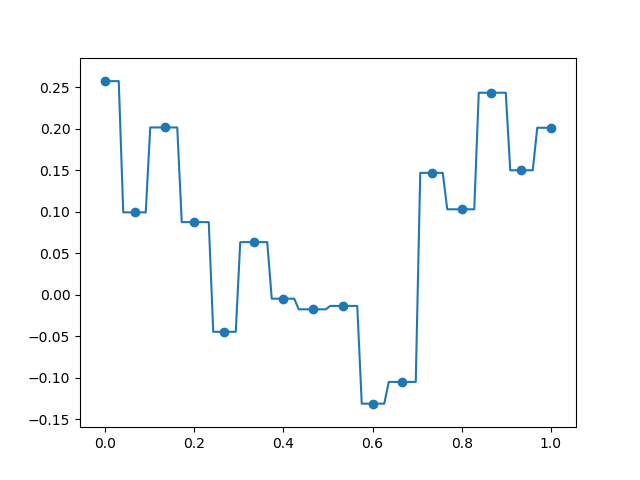
max_leaf_nodesをデータの個数-1と一緒にすると、
全ての訓練データを通るモデルを作ることができる。
訓練データに対しては100%の精度が出るが、未学習のデータに対して答えられなくなる(ほんとに？)。
これが過学習(overfitting)。
朝倉書店
売り上げランキング: 118,792