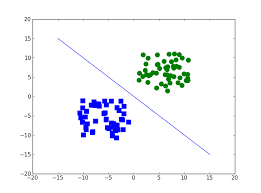
(x,y)平面上のサンプルデータ(xn,yn)が、(x,y)平面を分割する1次多項式f(x,y)=w0+w1x+w2y を基準に f(xn,yn)>0 であれば正解、f(xn,yn)<0であれば不正解 のいずれかに分類する問題を考える。
正解、不正解を表す変数tについて、正解の場合に+1、不正解の場合に-1としたとき、トレーニングデータ(xn,yn,tn)を与えて多項式の係数wを求める分類アルゴリズムをパーセプトロンという。
パラメトリックモデルの決定
(x,y)平面を分割する1次多項式f(x,y)を以下の通り定義する。
$$
f(x,y)=w_0+w_1x+w_2y
$$
トレーニングデータ(xn,yn)に対してパラメタtを以下の通り決定する。
$$
\begin{eqnarray}
f(x_n,y_n) > 0 \Rightarrow t=+1 \\
f(x_n,y_n) < 0 \Rightarrow t=-1
\end{eqnarray}
$$
tの符号とf(x,y)の符号の関係性から以下が言える。正解/不正解それぞれで場合分けして考えなくても良い。
f(xn,yn)>0なのにt=-1であるデータや、<0なのにt=+1であるデータは、以下の式より不正解として分類されるデータである。
$$
f(x_n,y_n)t > 0 \Rightarrow 正解 \\
f(x_n,y_n)t < 0 \Rightarrow 不正解
$$
モデルの評価式
トレーニングデータ(xn,yn,tn)を与えたとき、最良のパラメータw=(w0,w1,w2)を決めるため、多項式の評価式を決定する。正解、不正解を分類する問題であるから、全ての不正解データをf(x,y)に与えたときにその評価値が最小になるようにする。
これは、不正解データを無くすか、なるべく不正解データと距離が近いところを通るf(x,y)を見つけることに他ならない。ということで不正解データとの距離を定式化する。
$$
\begin{eqnarray}
E_n = | f(x_n,y_n) | \\
\end{eqnarray}
$$
不正解データについてのみEnを加算する。ただし (xn,yn)は不正解データのみ
$$
\begin{eqnarray}
E &=& \sum_n E_n = \sum_n |f(x_n,y_n)| \\
&=& -\sum_n (w_0 + w_1x_n+w_2y_n)t_n
\end{eqnarray}
$$
ここで、無理くりベクトル(行列))計算に持ち込む。
$$
\begin{eqnarray}
w &=& \left (
\begin{array}{c}
w_0 \\
w_1 \\
w_2
\end{array}
\right) \\
\phi &=& \left (
\begin{array}{c}
1 \\
x_n \\
y_n
\end{array}
\right) \\
E &=& -\sum_n t_nw^T\phi_n
\end{eqnarray}
$$
モデルの評価式Eが決まった。Eはwにより決まるためE(w)とも書ける。トレーニングデータからE(w)を最小化するパラメタを求めていく。
確率的勾配降下法
E(w)をwについて偏微分するとE(w)の勾配ベクトルを求められる。(あぁ線形代数…。E(w)の勾配ベクトル∇E(w)とは、ベクトルwにおいてE(w)を最大化する向きと大きさを持つベクトルのことです…)
$$
\begin{eqnarray}
\nabla E(w) &=& \left (
\begin{array}{c}
\frac{\partial E}{w_0} \\
\frac{\partial E}{w_1} \\
\frac{\partial E}{w_2}
\end{array}
\right ) \\
\end{eqnarray}
$$
一方、上のベクトルを微分すると以下の式となる。
$$
\nabla E(w) = – \sum_{n}t_n\phi_n
$$
E(w)の最小化を考えると以下が成り立つはず。
$$
\nabla E(w) = – \sum_{n}t_n\phi_n = 0
$$
∇E(w)はtとxを含むがwを含まず、∇E(w)を式変形してwの式に展開することができない。wの式に展開できないと∇E(w)を0にするwを求める式を立てられない。
そこで∇E(w)の幾何学的な特徴を利用した数値計算によりE(w)を更新する。勾配ベクトル∇E(w)はwにおいてE(w)を最も大きくするベクトルだから、wと-∇E(w)を加算することでE(w)を小さくできる。
これを繰り返し実行することでE(w)を最小化できる。
実際のトレーニングデータ数Nは大きく、∇E(w)の行列計算は大変な作業となる。そこで、トレーニングデータから無作為にデータを1個取り出し、その1個分のデータについてのみwを更新する。N=1のとき∇E(w)は以下の通りとなる。
$$
– \nabla E(w) = \sum_n t_n \phi_n = t_n \phi_n
$$
そのため、wの修正は以下の通りとなる。
$$
\begin{eqnarray}
w’ &=& w – ( -\nabla E(w) ) \\
&=& w + \nabla (Ew) \\
&=& w + t_n \phi_n
\end{eqnarray}
$$
E(w)が最小になるwが決まったとき、そのwを採用した多項式は、トレーニングデータについて誤りが少ない分類を行う式になっている。
トレーニングデータから無作為にサンプルを選んで勾配ベクトルの逆ベクトルを加算して降下していくから「確率的勾配降下法」という。へぇ。
パーセプトロンの収束速度
数値計算により値を更新していくアルゴリズムは、その収束速度が話題に上がる。パーセプトロンの確率的勾配降下法においてはトレーニングデータφのcにより調整する。
$$
\begin{eqnarray}
\phi &=& \left (
\begin{array}{c}
c \\
x_n \\
y_n
\end{array}
\right)
\end{eqnarray}
$$
確率的勾配降下法によりwを更新するときw0は1回の繰り返しで±cの範囲で増減する。cを大きくするとw0の増減範囲が大きくなり収束速度が速くなる。ではこのパラメータcはどのように決めるのか..はまた別のエントリで..。
$$
\begin{eqnarray}
w’ = w + t_n \phi_n
\end{eqnarray}
$$
分類アルゴリズムとして、パラメトリックモデルが線形でない場合や、そもそも教師無しの場合など、他にもいろいろあるので、別エントリに書いていく。