[mathjax]
sihoutteって何て読むのか...と思うけども\"シルエット\"だそう。フランス語源。
ポートレート写真を背景白、顔を黒に減色した例の\"シルエット\"。\"輪郭\"みたいな。
データ達を複数のクラスタに分割したとして、各々のデータがそのクラスタに存在することの
収まりの良さを表すことができる。
本来(相対的に)他のクラスタに属しているべきデータ達の割合が分かったり、
クラスタ境界で(相対的に)どちらのクラスタに属しても良さそうなデータ達の割合が分かったりする。
sklearnは教師なしクラスタリングまでで、それをグラフ化しないといけないのだけど、
matplotlibに対応するのがなく、\"線を書く\"みたいなコマンドを並べて作っていかないといけない様子。
yellowbrickというパッケージを使うとそれもやってくれる。
Yellowbrick is a suite of visual diagnostic tools called “Visualizers” that extend the Scikit-Learn API to allow human steering of the model selection process. In a nutshell, Yellowbrick combines scikit-learn with matplotlib in the best tradition of the scikit-learn documentation, but to produce visualizations for your models!
sklearnとmatplotloibだけで出力するバージョンと、yellowbrickで出力するバージョンの
両方を試してみた(前者はクラスタのラベルを出力できずsihoutteグラフとの対応関係が理解できずに
中途半端で終了)。
sihoutte係数
全データ達は(x_i)。データ(x_i)がクラスタ(A)に属し、最近傍にクラスタ(B)があるという状況。
(A)のクラスタ中心は(x_A)、(B)のクラスタ中心は(x_B)。
\"最近傍のクラスタ中心との距離の平均\"から\"自分のクラスタ中心との距離の平均\"を引いた値。
わざわざ1行に全ての変数が出てくるように書いてみる。
begin{eqnarray}
s_i = frac{sum_{i=1}^{n}|x_i-x_B|/n - sum_{i=1}^{n}|x_i-x_A|/n }{max bigl{sum_{i=1}^{n}|x_i-x_A|/n,sum_{i=1}^{n}|x_i-x_B|/n bigr}}
end{eqnarray}
データが(n)個あるので、sihoutte係数も(n)個できる。
自分が属しているクラスタ(A)よりも、隣のクラスタ(B)の方が居心地が良いと
分子はマイナスになる。
今属しているクラスタでも隣のクラスタでも、どちらもさほど居心地が変わらないとゼロ近辺になる。
大きければ迷いなく今のクラスタで良いことを表せる。
sklearnとmatplotlibだけでsihoutte係数
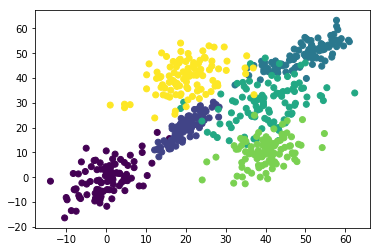
乱数で作った偽データに6-meansをかけた図。
どうやってもクラスタ中心のラベルが取り出せない!!..(スルー..)
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
mu = [[0,0], [20,20], [50,50], [40,30], [40,10], [20,40]]
sigma = [ [[30,20],[20,50]], [[20,30],[10,20]], [[60,40],[20,20]], [[60,20],[20,60]] ,[[30,10],[10,30]],[[50,20],[20,50]] ]
points = 100
clusters = []
for index in range(len(mu)):
cluster = np.random.multivariate_normal(mu[index], sigma[index], points)
dig = np.full((points,1),index+1, dtype=int)
cluster = np.hstack((cluster,dig))
clusters = np.r_[clusters,cluster] if len(clusters) > 0 else cluster
plt.scatter(x=clusters[:,0], y=clusters[:,1],c=clusters[:,2])
from sklearn.cluster import KMeans
model = KMeans(n_clusters=6, init=\'random\',max_iter=10)
y_km = model.fit_predict(clusters[:,:2])
labels = model.labels_
centers = model.cluster_centers_
centers
fig = plt.figure()
ax1 = fig.add_subplot(1,1,1)
ax1.scatter(x=clusters[:,0], y=clusters[:,1],c=labels)
ax2 = fig.add_subplot(1,1,1)
ax2.scatter(x=centers[:,0], y=centers[:,1], alpha=0.5,s=600,c=\"pink\",linewidth=2,edgecolors=\"red\")
sklearnとmatplotlibだけでsihoutte係数のグラフを出してみる。
\"線を書く\"みたいなコマンドを並べて規格通りの図を作るのか...。
from sklearn.metrics import silhouette_samples
# cluster数
num_clusters=6
#全データのsilhouette係数を取得
silhouette_vals = silhouette_samples(clusters[:,:2],y_km,metric=\'euclidean\')
cluster_labels = np.unique(y_km)
min,max = 0,0
yticks = []
for i,c in enumerate(cluster_labels):
c_silhouette_vals = silhouette_vals[y_km == c]
c_silhouette_vals.sort()
max += len(c_silhouette_vals)
plt.barh(
range(min,max),
c_silhouette_vals,
height=1.0,
edgecolor=\'none\'
)
yticks.append((min+max)/2.)
min += len(c_silhouette_vals)
avg = np.mean(silhouette_vals)
plt.axvline(avg, color=\'red\', linestyle=\"--\")
plt.yticks(yticks, cluster_labels + 1)
plt.ylabel(\'Cluster\')
plt.xlabel(\'Silhouette coefficient\')
plt.show()
全体的に茶色のクラスタのsilhouette係数が低め。
残念ながら、どのクラスタと対応するのか出力できず何の考察も出来ず...。
yellowbrickでsilhouette係数を出力
無茶苦茶簡単に出せる。
from yellowbrick.cluster import SilhouetteVisualizer
sv = SilhouetteVisualizer(model)
sv.fit(clusters[:,:2])
sv.poof()
出てきた図。自作したものと全然合っていないように見える..
自作したものとラベルが合っていないだけだと信じたい。
似た形の塊があるので..
以上、完全な失敗だけれども一旦終了...