マルコフ連鎖モンテカルロ法。2変量正規分布からGibbs Samplingする方法を考えてみました。
式を流してもよくわからないので、行間ゼロで理解できるまで細切れにして書いてみます。
Gibbs Sampling
無茶苦茶一般的に書かれている書籍だと以下みたいになっている。
ステップごとに\(\theta=(\theta_1,\theta_2,\cdots,\theta_n)\)の各要素を、
その要素以外の要素の条件付き確率でランダムに発生させる。
\begin{eqnarray}
\theta^0 &=& (\theta_1^0,\theta_2^0,\cdots,\theta_n^0) \\
\theta_i^{t+1} &\sim& p(\theta_i|\theta_1^{t+1},\cdots,\theta_{i-1}^{t+1},\theta_{i+1}^t,\cdots,\theta_n^t)
\end{eqnarray}
2次元空間であれば、ある点を決める際に、
片方の変数\(\theta_1\)を固定して条件付き確率\(P(\theta_2|\theta_1)\)を最大にするパラメタ\(\hat{\theta_2}\)を決める。
その時点で\((\theta_1,\hat{\theta_2})\)が決まる。
次は変数\(\hat{\theta_2}\)を固定して条件付き確率\(P(\theta_1|\hat{\theta_2})\)を最大にするパラメタ\(\hat{\theta_1}\)を決める。
2次元正規分布であれば、片方の確率変数を固定したときの条件付き確率が1変数の正規分布になるから、
これがすごくやりやすい。
Gibbs Samplingは、このように条件付き確率を計算できる必要がある。
2変量正規分布の条件付き確率
2変量正規分布の片方の確率変数を固定すると1変数の正規分布が出てきます。
山の輪切りにして出てきた正規分布の母数を調べたいのですが、導出が無茶苦茶大変そうです。
出てきた正規分布の母数について式変形すると出てくるようです。こちらを参考にさせて頂きました。
この関係式を利用してひたすら式変形していきます。
\begin{eqnarray}
f(x|y) &=& \frac{f(x,y)}{f(x)}
\end{eqnarray}
今、確率変数\(y=y’\)を固定し確率変数\(x\)の正規分布を考えます。
2変量正規分布の分散共分散行列が\(\sum\)であるとします。
\begin{eqnarray}
\sum &=& \begin{pmatrix}
\sigma_{xx} & \sigma_{xy} \\
\sigma_{yx} & \sigma_{yy}
\end{pmatrix}
\end{eqnarray}
出てくる正規分布の平均は以下となります。
確率変数が\(x\)なのに固定した\(y\)が出てくるのがポイント。
\begin{eqnarray}
\mu’ = \bar{x} + \frac{\sigma_{xy}}{\sigma_{yy}} (y’-\bar{y})
\end{eqnarray}
また、出てくる正規分布の分散は以下となります。
\begin{eqnarray}
\sigma’^2 &=& \sigma_{xx} – \frac{\sigma_{xy}}{\sigma_{yy}} \sigma_{yx}
\end{eqnarray}
Python実装例
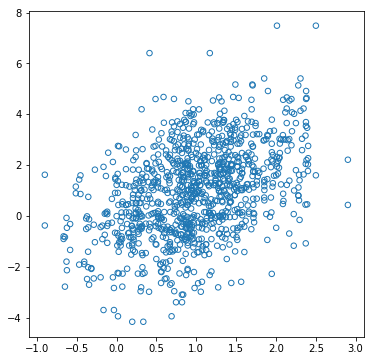
実際にPythonコードにしてみた図です。2変量正規分布の条件付き確率さえわかってしまえば
あとはコードに落とすだけです。
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
n_dim = 2
def gibbs_sampling(mu, sigma, sample_size):
samples = []
start = [0, 0]
samples.append(start)
search_dim = 0
for i in range(sample_size):
search_dim = 0 if search_dim == n_dim-1 else search_dim + 1
prev_sample = samples[-1][:]
s11 = sigma[search_dim][search_dim]
s12 = sigma[search_dim][search_dim - 1]
s21 = sigma[search_dim -1 ][search_dim]
s22 = sigma[search_dim - 1][search_dim - 1]
mu_x = mu[search_dim]
mu_y = mu[search_dim-1]
_y = prev_sample[search_dim - 1]
new_mean = mu_x + s12/float(s22) * (_y - mu_y)
new_sigma = s11 - s12/float(s22) * s21
sample_x = np.random.normal(loc=new_mean, scale=np.power(new_sigma, .5), size=1)
prev_sample[search_dim] = sample_x[0]
samples.append(prev_sample)
return np.array(samples)
nu = np.ones(2)
covariance = np.array([[0.5, 0.5], [0.5, 3]])
samples = gibbs_sampling(nu, covariance, 1000)
fig, ax1 = plt.subplots(figsize=(6, 6))
ax1.scatter(sample[:, 0], sample[:, 1],
marker="o", facecolor="none", alpha=1., s=30., edgecolor="C0", label="Samples"
)
実行結果
