-
-
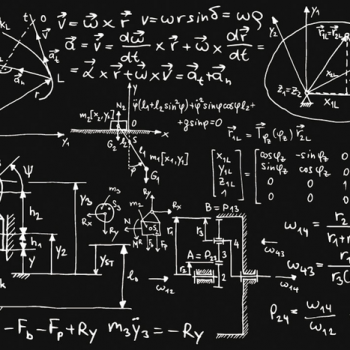
最尤推定とベイズの定理とMAP推定
最尤推定とMAP推定とベイズの定理は繋がっていたので、 記憶が定かなうちに思いの丈を書き出してみるテスト。俯瞰してみると面白い。 あるデータ達\(x\)が観測されていて、それらは未知のパラメータを持つ …
-

-
正規分布に従う確率変数の二乗和はカイ二乗分布に従うことを実際にデータを表示して確かめる
以前、”正規分布に従う確率変数の二乗和はカイ二乗分布に従うことの証明”という記事を書いた。 記事タイトルの通り、正規分布に従う確率変数の二乗和はカイ二乗分布に従う。 実際にデー …
-

-
PHP7.4の新仕様 … PHP RFC: FFI – Foreign Function Interface
2019/08/09 -PHP
PHP7.4の新仕様 FFI,Foreign Function Interface について。Python的な…。 PHP7の時点で既にバイトコードになっていてPHP8からJITによるネイ …
-

-
vagrant userがdockerに入門するためのチートシート
vagrantを知っていてこれからdockerに入門する方向のチートシートを書く。 dockerコンテナの方が小さいので基本的に粒度が合わないが、 対称性を重視して似た機能を並べてみた。 コマンド一覧 …
-
-
tmux – ssh接続先をtmuxのペインに表示する
昔使っていた.tmux.confが失われてしまったため、新しいものを作っていく。 不要な機能が満載になっていたので、これを機に必要なものだけ設定する。 複数の鯖にsshで繋ぐと、ssh接続のペインだら …
-

-
n次元超球体の体積
2019/08/05 -情報科学
球面集中現象理解のための数学シリーズ第2弾。 前の記事でデカルト座標->極座標の変換から体積要素の積分により3次元球体の体積を導出してみました。 極座標の3変数\(r,\phi_1,\phi_2\)に …
-

-
PHPで統計アプリを作れるか否か
LaravelをAPIサーバにして同期的にsklearnのPCAを実行するアプリを作ってみました。 jQyery/bootstrap/chart.jsがフロント、APIサーバはLaravel+MySQ …
-

-
球面集中現象を理解するために必要そうなことの理解 – 極座標・直行座標変換,
球面集中現象を理解するために記憶にないことが多すぎるので 理解に必要そうなことを少しずつ復習していきます。 まず極座標の直行座標変換。極座標を使って球の体積を求めてみます。 次の記事で球の体積を求める …
-

-
sklearnとmatplotlibでsihoutte係数を見てみようとして失敗した話とyellowbrick
sihoutteって何て読むのか…と思うけども”シルエット”だそう。フランス語源。 ポートレート写真を背景白、顔を黒に減色した例の”シルエット̶ …
-

-
エルボー法とは , サンプルデータへの適用例
k-means法を実行する際に妥当なkを決めたいという欲求があります。 クラスタ集合の凝集度を定量化することでkと凝集度の関係を得られます。 複数のkについてkと凝集度の関係を取得し、 そこから妥当な …
