データセットのバラツキを縮約する統計量である分散と標準偏差について、
単なる概念ではなくて、直感的な理解の助けになる読み物を読んだのでまとめてみる。
偏差\( \sigma^2 \) とは平均 \( \bar{x} \) との距離 \( x_i – \bar{x} \)のことを言う。
以下のように偏差の平均を式変形するとゼロになる。
$$
\begin{eqnarray}
\frac{1}{N} \sum_{i}^{N} \sigma^2 &=& \frac{1}{N}\sum_{i}^{N}( x_i – \bar{x} ) \\
&=& \frac{1}{N} \left( \sum_{i}^{N}x_i – N \bar{x} \right) \\
&=& \frac{1}{N} \sum_{i}^{N}x_i – \frac{N}{N} \bar{x} \\
&=& \bar{x} – \bar{x} \\
&=& 0
\end{eqnarray}
$$
距離 \( x_i – \bar{x} \) の平均がゼロになるところに平均\( \bar{x} \) があるイメージ。
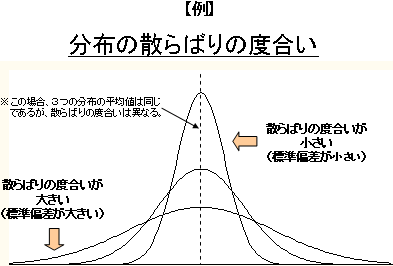
データセットのバラツキを調べるために偏差の平均を使うと、
平均を挟んでプラスとマイナスが打ち消しあってしまうから、
プラスとマイナスを打ち消し合わないように2乗の平均を使おう
というのが基本的なアイデア。
$$
\begin{eqnarray}
v &=& \sigma^2 \\
&=& \frac{1}{N} \sum_{i}^{N}(x_i-\bar{x})^2
\end{eqnarray}
$$
2乗の平均だとデータセットのデータの単位が2乗されていて大きすぎるから、
データセットのデータの単位に合わせるためにルートをとる。それが標準偏差。
$$
\begin{eqnarray}
\sigma &=& \sqrt{ \frac{1}{N} \sum_{i}^{N}(x_i-\bar{x})^2}
\end{eqnarray}
$$
標準偏差によりデータセットのバラツキをデータの同じ次数で表現できる。
文部科学省 用語解説より引用
データの値の離れ具合(散らばりの度合い)を表す数値。分散(「データの平均と個々のデータの差」の2乗の平均)の平方根で求められ,標準偏差が0とは,ばらつきがない(データの値がすべて同じ)ことを意味する。